你是否曾好奇,數字世界中最「孤獨」的基石是什麼?本文深入探索「質數」的奧秘,從其定義、獨特的「算術基本定理」,到在現代「加密」技術中的關鍵應用,以及至今仍未解的數學「謎題」。一同揭開這些宇宙原子般的數字,如何形塑我們的數位世界,並持續挑戰人類智慧的極限。
【質數的孤獨告白:宇宙的原子】

什麼是質數?為何1不是質數?
H4 質數與合數的定義
在數字的王國裡,成員們可以被簡單地分為兩類。想像一下,每個大於1的數字都想用更小的數字積木來搭建自己。有些數字,像是 4 (2×2)、6 (2×3) 或 9 (3×3),可以由其他積木組合而成,我們稱之為「合數」(Composite Numbers),因為它們是「合成」的。
然而,有一些數字天生孤傲,無法被任何比自己小的數字(除了1之外)整除。它們就像宇宙中最基本的粒子,無法再被分割。這些數字,例如 2、3、5、7、11,它們的因數只有 1 和自己本身,這就是大名鼎鼎的「質數」(Prime Numbers)。它們是構成所有數字的基石。
H4 數字1的特殊身份:單位
那麼,數字 1 呢?它只有一個因數(就是1自己),這讓它既不符合質數(恰好兩個因數)的定義,也不符合合數(三個或更多因數)的定義。但將 1 排除在質數家庭之外,還有一個更深刻、更關鍵的理由。
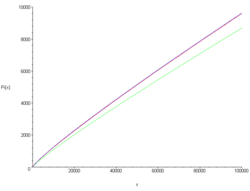
數學家們發現了一條宇宙級的定律,稱為「算術基本定理」(Fundamental Theorem of Arithmetic)。這條定理論斷:任何一個大於 1 的整數,要嘛本身就是一個質數,要嘛可以被寫成一串質數的乘積,而且這種寫法是獨一無二的!例如,12 只能分解成 2 × 2 × 3,絕無其他可能。
現在,讓我們做個思想實驗:如果我們頑固地把 1 當作質數,會發生什麼?那麼 12 的分解就會變成一場災難:
- 12 = 2 × 2 × 3
- 12 = 1 × 2 × 2 × 3
- 12 = 1 × 1 × 2 × 2 × 3
- …
分解的方式將有無限多種,那條神聖的「唯一性」定律就此崩潰。為了維護數字世界的秩序與和諧,數學家們一致同意,1 不屬於質數,它擁有一個獨特的稱號:「單位」(Unit)。
數字中的異類:唯一的偶質數2
H4 為何2是所有質數中最奇特的?
在無窮無盡的質數星海中,幾乎所有的星星都閃爍著「奇數」的光芒,唯獨一顆例外,它就是數字 2。
2 是所有質數中唯一的偶數。這個身份看似簡單,卻賦予了它極其特殊的地位。道理很直白:任何一個大於 2 的偶數(4, 6, 8, 10…)根據定義都可以被 2 整除,因此它們除了 1 和自身之外,必然還有一個因數是 2。這意味著它們自動失去了成為質數的資格,淪為合數。
於是,2 成了偶數世界裡唯一的質數倖存者,一個獨一無二的存在。它就像一位站在奇數與偶數邊界上的孤獨哨兵,這個獨特性質是數論研究的基石之一,即便到了 2025 年,數學家們依然對此深深著迷。從某個角度來看,儘管 2 是唯一的偶質數,但它卻是所有質數中最「奇特」的一個。
【算術基本定理:所有數字的唯一DNA】
萬物皆數,數皆質數
什麼是算術基本定理?
如果說質數是構成數字宇宙的基本原子,那麼「算術基本定理」就是支配這個宇宙的根本大法。這條定理由古希臘的歐幾里得首次證明,它揭示了一個深刻而優美的真相:任何一個大於1的整數,要嘛本身就是一個質數,要嘛可以被分解成一串質數的乘積,而且這種分解方式是獨一無二的,就像每個生物都擁有獨一無二的DNA序列。
質數,正是乘法世界裡最基礎的磚塊。數字12的DNA是「2, 2, 3」,而99的DNA是「3, 3, 11」。無論你用何種順序或方法去拆解,最終得到的質數零件組合永遠是這一套,絕無例外。這個看似簡單的定理是數論的基石,其重要性歷久不衰,即便到了2025年,它依然是所有數字理論的起點。
案例:拆解數字2520
讓我們以一個有趣的數字2520為例,來見識一下這條定理的威力。2520是從1到10所有數字的最小公倍數,這讓它在古代就備受關注。它的質因數分解(或稱標準分解式)是什麼呢?
答案是:2³ × 3² × 5¹ × 7¹
這串「DNA」不僅告訴我們2520的構成,還隱藏了更多秘密。例如,我們想知道2520總共有多少個正因數(可以整除它的數),不必一個個去試除。利用它的質因數分解,我們可以施展一個數學魔法:將每個質因數的次方數加1,然後再相乘。
(3+1) × (2+1) × (1+1) × (1+1) = 4 × 3 × 2 × 2 = 48
答案瞬間揭曉:2520不多不少,恰好有48個正因數。這正是算術基本定理展現出的既深刻又實用的力量。
歷史的迴響:為何質數在中國古算中缺席?
古希臘的「原子論」思想
質數概念的誕生,與古希臘的哲學思想密不可分。深受德謨克利特「原子論」的影響,古希臘數學家傾向於將世界萬物看作由不可分割的最小單元構成。他們將這種思想投射到數字上:數字1是構成所有數字的「單位」(Unit),而那些無法被更小數字(除了單位1)乘積而成的數,自然就是「質數」,如同數字世界裡的「原子」。這種自下而上的建構式思維,為質數理論奠定了哲學基礎。
中國古算的「數根」概念
與此相對,中國古代數學的發展走了一條截然不同的道路。傳統算學更注重解決實際問題,例如測量、曆法和稅收,發展出許多高超的計算技巧與演算法,但較少探究數字背後的抽象哲學體系。因此,儘管古算中不乏對因數分解的應用,卻始終沒有形成與古希臘對應的「質數」概念。
直到清朝康熙年間,由西方傳教士與中國學者共同編纂的數學百科全書《數理精蘊》出版,才正式將質數的概念系統性地引入中國。書中將質數翻譯為一個非常貼切的名字——「數根」,意指它們是構成所有數字的根本。這個詞彙,也恰如其分地道出了質數在數字世界中的核心地位。
【尋找質數的蹤跡:它們有規律嗎?】
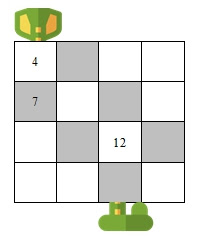
質數會越來越稀有,但永不消失
隨著數字越來越大,質數的出現頻率確實會逐漸降低,像是沙漠中的綠洲一樣越來越罕見。然而,它們永遠不會完全消失。這個驚人的事實,早在兩千多年前就已被證明。
歐幾里得的千年證明:質數有無限多個
這個證明是數學史上最優美的論證之一,由古希臘數學家歐幾里得提出,其巧妙之處至今仍令數學家讚嘆。他運用的是一種稱為「反證法」的邏輯技巧:
- 先大膽假設結論是錯的:讓我們假設質數是有限的,存在一個「最大」的質數,我們稱之為 P。
- 構造一個全新的數字:現在,我們把從2開始一直到 P 的所有質數全部乘起來,然後再加上1。得到一個巨大的新數字 N = (2 × 3 × 5 × … × P) + 1。
- 提出關鍵問題:這個 N 是質數還是合數?
- 如果我們用任何一個已知的質數(從2到P)去除 N,會發現餘數永遠是 1。這意味著 N 不可能是由任何我們已知的質數構成的合數。
- 因此,只剩下兩種可能:要嘛 N 本身就是一個比 P 更大的新質數;要嘛 N 可以被一個比 P 更大的未知質數整除。
- 推翻最初的假設:無論是哪種情況,我們都找到了一個比 P 更大的質數。這與我們最初「P是最大質數」的假設相矛盾。因此,最初的假設是錯誤的,結論只能是:質數沒有上限,它們是無限的。
質數沙漠:尋找連續的合數
儘管質數無窮無盡,但它們之間的間隔卻可以變得任意大。我們可以構造出一段很長的、完全由合數組成的「質數沙漠」。想找一段連續99個合數嗎?方法如下:
首先,計算「100的階乘」,也就是 100! = 1 × 2 × 3 × … × 100。這是一個能被2到100之間所有整數整除的龐大數字。接著,觀察下面這個數列:
- 100! + 2 (可以被 2 整除)
- 100! + 3 (可以被 3 整除)
- 100! + 4 (可以被 4 整除)
- …
- 100! + 100 (可以被 100 整除)
從 100!+2 到 100!+100,這連續的99個數字,每一個都是合數。透過這個方法,理論上我們可以構造出任意長度的「質數沙漠」,無論是一百萬、還是一億個連續的合數。這也揭示了質數分佈的另一個奇特性:它們在數線上無限延伸,卻又可能離得非常遙遠。
質數的「身分證」:費馬小定理
在茫茫數海中,要如何快速判定一個極大的數是不是質數?一個個去找它的因數太過費力。幸運的是,17世紀的法國數學家費馬發現了一把神奇的鑰匙,為質數提供了一種有效的「身分證驗證」方法。
如何快速檢驗一個大數不是質數?
費馬小定理是一個篩選合數的強大工具。其內容是:如果 p 是一個質數,那麼對於任意整數 a(此處為簡化,我們用2),「2 的 (p-1) 次方減 1」,即 2ᵖ⁻¹ – 1,必然可以被 p 整除。
這個定理反過來用就變得非常實用:如果一個數 n,它無法整除 2ⁿ⁻¹ – 1,那麼這個數 n 就絕對不是質數。
例如,想知道數字 21 是否為質數。我們計算 2²⁰ – 1,會發現它無法被 21 整除。於是,我們不必費力去尋找 3 或 7 這樣的因數,就能立刻判定 21 是個合數。在2025年的今天,這個原理經過強化與演變,已成為現代密碼學中質數測試演算法的基礎。
偽質數的挑戰
然而,費馬小定理也帶來了一個有趣的挑戰:如果數字 n 通過了這個檢驗,它就一定是質數嗎?答案是:不一定。
有些合數非常狡猾,它們雖然不是質數,卻能通過費馬小定理的檢驗。這種「偽裝」成質數的合數被稱為「偽質數」。歷史上第一個被發現的偽質數是 341。
- 341 是個合數,因為 341 = 11 × 31。
- 但是,當我們計算 2³⁴⁰ – 1 時,會驚訝地發現這個龐大的數字確實可以被 341 整除。
341 就像一個拿著假身分證的冒牌貨,成功騙過了費馬的初步檢驗。這些偽質數的存在,提醒著數學家們,尋找質數的道路上充滿了意想不到的陷阱與驚喜,也促使他們發展出更為複雜和精確的質數判定方法。
【從數學謎題到億萬產值:質數的驚人應用】

數位世界的守護神:加密演算法
質數不僅是數學家們的迷人玩具,更是撐起現代數位世界安全基石的巨人。從前一章我們看到,要判斷一個數是不是質數,本身就是一大挑戰。而數學家們巧妙地利用了質數世界的另一項特性——「單向操作的困難性」,打造出保護我們資訊安全的強大盾牌。
RSA加密演算法的核心
現代最廣泛使用的加密技術之一,RSA演算法,其核心原理可以用一句話來概括:將兩個極大的質數相乘非常容易,但要將它們的乘積拆解回原來的兩個質數,則困難到幾乎不可能。
想像一下,給你兩個各有數百位數的質數,即使是普通的電腦也能在瞬間計算出它們的乘積。然而,如果只告訴你這個龐大的乘積結果,並請你找出當初是哪兩個質數相乘得來的,這趟「逆向工程」將會是一場惡夢。以2025年的頂尖超級電腦來計算,破解這個謎題可能需要花上數千年甚至更久的時間。這種計算上的不對稱性,就像一條數學世界的單行道,構成了加密技術的基礎。
為何你的網路交易如此安全?
當你在網路上進行轉帳、購物或傳送私密訊息時,正是質數在默默守護你的安全。在RSA這類「公開金鑰加密」系統中,那個由兩個大質數相乘得到的龐大數字,可以作為「公鑰」對外公開。任何人都可以用這把公鑰將資訊「上鎖」(加密)。
然而,要將這些加密後的資訊「解鎖」(解密),則必須使用由那兩個原始質數構成的「私鑰」。由於分解公鑰找出私鑰在計算上是行不通的,因此只有持有私鑰的接收者(例如銀行或通訊軟體伺服器)才能讀取資訊的真實內容。這個基於大質數分解難題的演算法,已成為全球金融交易與資訊通訊安全的標準配備,確保了數位世界的隱私與信任。
追求完美的數字:完全數的奧秘
質數的影響力不僅展現在尖端科技,也延伸到古典數學中最優雅的謎題之一:尋找「完全數」(Perfect Number)。這個追求「完美」的古老問題,其答案竟也與質數緊密相連。
什麼是完全數?
一個正整數如果等於它所有真因數(即除了自身以外的因數)的總和,就被稱為「完全數」。古希臘的數學家們最早發現了它們,並為其和諧的特性深深著迷。它們在數線上極為罕見,是數字中的珍寶。
- 最小的完全數是 6,它的真因數為 1、2、3,而
1 + 2 + 3 = 6。 - 下一個完全數是 28,其真因數為 1、2、4、7、14,而
1 + 2 + 4 + 7 + 14 = 28。
完全數與質數的連結
歷經數個世紀的探索,數學家們發現了一條尋找完全數的黃金定律,而這條定律的關鍵角色,正是一種特殊的質數。
歐幾里得首先證明,如果 2ⁿ−1 是一個質數,那麼 2ⁿ⁻¹ × (2ⁿ−1) 這個數必定是個完全數。後來,歐拉更進一步證明了所有已知的偶完全數都必須符合這個公式。這裡的 2ⁿ−1 型質數,正是我們在質數探索中會遇到的「梅森質數」。
- 當 n=2,
2²−1 = 3是個梅森質數。此時產生的完全數為2²⁻¹ × (2²−1) = 2¹ × 3 = 6。 - 當 n=3,
2³−1 = 7是個梅森質數。此時產生的完全數為2³⁻¹ × (2³−1) = 2² × 7 = 28。
因此,每當人們發現一個新的梅森質數,就意味著同時發現了一個新的、更巨大的完全數。然而,這個完美的連結也留下了一個懸而未決的千年之謎:至今發現的所有完全數都是偶數。是否存在「奇完全數」?這是數學界最古老、也最著名的未解問題之一,持續吸引著無數數學愛好者投入探索。
【三大未解猜想:數學家們的聖母峰】

哥德巴赫猜想:偶數的終極浪漫
猜想內容:任一大於2的偶數都是兩質數之和
在質數的世界裡,有些問題看似簡單,卻像高聳的山峰,一個多世紀以來無人能完全征服。「哥德巴赫猜想」就是其中最著名的一座。這個猜想的敘述極其簡潔,連中學生都能輕易理解:任何一個大於 2 的偶數,都可以表示成兩個質數的和。
4 = 2 + 28 = 3 + 5100 = 3 + 97
這個在 1742 年提出的猜想,至今仍是未解之謎。儘管數學家們已經透過電腦驗證了對極其巨大的數字(高達 4×10¹⁸)都成立,但這在嚴謹的數學世界裡,並不能算是「證明」。它就像一句關於數字的浪漫宣言,美麗、簡潔,卻始終等待著一個無懈可擊的邏輯來證實其永恆的真實性。
科學新知:奇數哥德巴赫猜想的突破
雖然偶數的猜想依然懸而未決,但它的「兄弟問題」——奇數哥德巴赫猜想,卻在近年迎來了歷史性的突破。2013 年,秘魯數學家哈洛德·賀歐夫各特(Harald Helfgott)提交了論文,完整證明了「弱哥德巴赫猜想」,即每一個大於 7 的奇數,都可以寫成至多三個奇質數的和。這項成就被視為數論領域的里程碑,也為最終攻克那個關於偶數的「強猜想」帶來了新的希望。
孿生質數:數學界的傳奇與張益唐
什麼是孿生質數?
在無窮無盡的質數數列中,有時會出現一些有趣的現象。有些質數是孤單的,但有些卻喜歡成雙成對地出現,它們之間的距離僅僅為 2。數學家將這些緊密相鄰的質數對稱為「孿生質數」(Twin Primes)。
例如 (3, 5)、(5, 7)、(11, 13)、(17, 19) 都是孿生質數。隨著數字越來越大,質數本身變得稀疏,孿生質數也越來越罕見。一個困擾數學家們數百年的問題是:這樣的質數對會不會在某個數字之後就永遠消失了?還是它們會一直、無限地出現?
張益唐的突破:從7000萬到246
這個關於孿生質數是否有無限對的猜想,同樣是數學界的聖母峰之一。長久以來,它始終沒有實質性進展。直到 2013 年,這個僵局被當時名不見經傳的華裔數學家張益唐打破。
張益唐證明了,即使我們無法確定孿生質數(間距為 2)是否無限,但確實存在無限多組質數對,它們之間的間距不超過一個固定的數。他給出的這個上限是 7000 萬。這個數字雖然巨大,但它首次從「無限」的迷霧中,為質數的間距問題劃定了一個有限的邊界。
張益唐的論文猶如平地驚雷,引發了全球數學界的震動與合作熱潮。在隨後的幾個月裡,包括陶哲軒在內的許多頂尖數學家,透過「博學者計畫」(Polymath Project)線上協作,不斷縮小這個間距上限。在眾人的努力下,這個數字最終從 7000 萬被大幅縮減至 246。這意味著,存在無窮多對質數,它們的差距小於 246。這項從 0 到 1 再到更精確的突破,是人類在理解質數分佈奧秘的道路上,邁出的巨大一步。
【數學之美:像葛登能一樣思考】
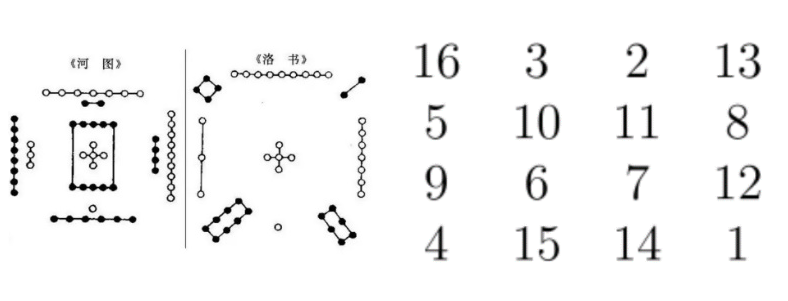
在前一章節,我們仰望了數論領域中那些如聖母峰般宏偉的猜想。但數學的美,不僅僅存在於那些等待數百年證明的頂級難題中。它同樣隱藏在一些看似簡單、實則充滿巧思的趣味謎題與悖論裡,等待著一顆好奇心去發掘。這正是傳奇數學科普作家葛登能(Martin Gardner)為我們揭示的道路:數學,首先應該是一場有趣的智力遊戲。
趣味數學:為何所有整數都很有趣?
你或許會覺得,有些數字,比如 7 或 13,因為它們的文化或數學特性而顯得「有趣」;而像 361 或 5,824 這樣的數字,似乎就平凡無奇。但一個經典的趣味數學論證將告訴你:世界上不存在「無趣」的整數。
一個讓你腦洞大開的趣味證明
這個證明採用了數學中一種經典的論證方法:反證法。
讓我們姑且「假設」存在一個由「最無趣的整數」組成的集合。如果這個集合不是空的,那麼根據良序原則(任何非空正整數集合中必有一個最小的數),這個集合裡必然存在一個「最小的、最無趣的數字」。我們稱它為 N。
現在,請思考一下 N 的獨特性質:它是「第一個最無趣的數字」。這個頭銜本身是不是就賦予了 N 一個極其特殊的、引人注目的屬性?畢竟,在無窮的數字海洋中,成為「第一個無趣者」,這本身就是一件非常有趣的事!
於是,我們陷入了一個邏輯悖論:數字 N 因為它的「無趣」而變得「有趣」。這與我們最初的假設——N 是一個無趣的數字——相矛盾。因此,我們最初的假設「存在無趣的整數」必定是錯誤的。結論就是:所有的整數都很有趣。
數學教育的反思:不該只有無聊的計算
這個關於有趣數字的證明,雖然像個文字遊戲,卻精準地體現了一種重要的數學思維。它也引導我們反思:在 2025 年的今天,我們的數學教育是否過於專注在枯燥的計算與公式上,而忽略了其背後的趣味與智慧?
葛登能的啟示:在遊戲與謎題中探索數學
科普巨擘葛登能(Martin Gardner)一生致力於向大眾展示數學的另一面。他本人並非專業數學家,而是一位充滿熱情的作家與魔術師。他擅長將深奧的數學原理,巧妙地融入到謎題、悖論、棋盤遊戲和紙牌魔術中。他讓我們明白,數學的核心不是反覆運算,而是一種思維的藝術,一種在規則中尋找自由與創意的探索。
讓數學變得好玩的重要性
當數學被呈現為一系列必須記憶的規則與繁瑣的習題時,很容易讓人望而生畏,進而產生「數盲」(Innumeracy)現象——對數字和邏輯感到隔閡與無力。然而,透過葛登能式的趣味探索,例如悖論、邏輯謎題或策略遊戲,學習者可以在輕鬆的氛圍中,自然地鍛鍊邏輯推理能力,理解抽象概念,並真正感受到發現規律與解決問題時所帶來的喜悅。這不僅能提升數學素養,更能培養一種受用終身的、清晰而富有創造力的思維方式。
質數:貫穿數字宇宙的無限奧秘
質數是數字世界的「原子」,僅有1和自身為因數,而1因「算術基本定理」的唯一性而不屬質數,2則是唯一的偶質數。「算術基本定理」確立了每個大於1的整數都能唯一分解成質數乘積,是數論基石。質數雖然隨著數字增大而稀疏,但「歐幾里得證明」了其無限性,同時也存在任意長的「質數沙漠」。
「費馬小定理」提供質數檢驗方法,但也存在「偽質數」的挑戰。質數在現代科技中扮演「數位世界的守護神」,「RSA加密演算法」利用其分解困難性保障網路安全。它們也與「完全數」的發現緊密相連,歐拉公式揭示了偶完全數與梅森質數的關係。
「哥德巴赫猜想」和「孿生質數猜想」是數論的「聖母峰」,張益唐等數學家的突破為這些千年謎題帶來曙光。最後,文章強調了「趣味數學」的重要性,鼓勵像葛登能一樣,在遊戲與謎題中探索數學之美,培養邏輯思維,而非僅限於枯燥計算。


